|
anti-gravity matter > evidence simulation
of a galaxy in anti-gravity matter |
|
|
1) The simulation contains many anti-gravity matter particles. They spread themselves out throughout space with even density. Notes 1.1) The simulated space is a sphere of about 4.5 units radius. 1.2) Each view is of a 2 units thick slice through the centre of the sphere. 1.3) When the energy of the anti-gravity matter particles is low they arrange themselves in shells. 1.4) Anti-gravity matter particles are held within the simulated space by the addition of an extra force pushing each particle towards the centre and proportional to its distance from the centre. This simulates the force they would feel from anti-gravity matter spread evenly throughout the rest of the universe. This is explained further in the Basic Maths page. |
|
|
2) A massive normal matter particle is added fixed at the centre. The anti-gravity matter particles are repelled from it and an AGM Boundary is formed. In the simulation the AGM Boundary is at a radius of about 2 units. The anti-gravity matter particles do not require any orbital velocity to remain in equilibrium outside the AGM Boundary. The density of the anti-gravity matter particles outside the AGM Boundary is constant (** see below) and unchanged so the volume of simulated space is slightly increased. |
|
|
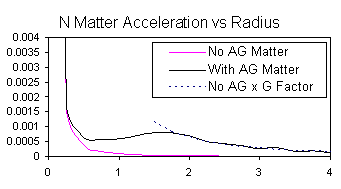
3) The gravity profile around the normal matter object is affected by the anti-gravity matter. The total gravity is the sum of the gravity of the normal matter object plus the gravity of the anti-gravity matter hole. The gravity of the anti-gravity matter hole is like that of a constant density normal matter object the same size as the AGM Boundary. It increases with radius up to the AGM Boundary and then decreases according to the inverse square law. Outside the AGM Boundary a normal matter particle feels the gravity multiplied by a constant factor as explained in the Basic Maths page. . G Factor = Notes 3.1) The plot shows the acceleration that would be experienced by a small free Normal matter particle as its radius changed. 3.2) 20 runs of the simulation were averaged. The measured acceleration profile is affected by the fact that in the simulation the anti-gravity matter particles tend to settle into shells. However after accounting for this it fits the prediction. |
|
|
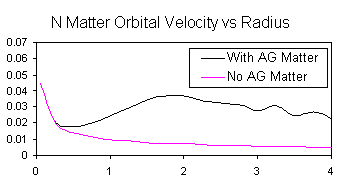
4) The velocity required by a small normal matter particle to remain in a circular orbit around the central particle is also affected by the anti-gravity matter. The peak in the orbital velocity profile is around the radius of the AGM Boundary. Notes 4.1) The outer end of the orbital velocity profile is affected by the fact that in the simulation the Anti-gravity matter particles tend to settle into shells. |
|
|
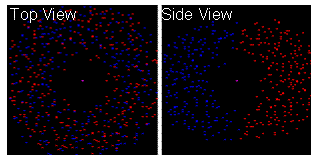
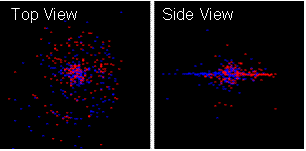
5) If the anti-gravity matter is given some orbital velocity it moves outwards at the equatorial plane and reduces in density close to the AGM Boundary. That reduction in density changes the gravity profile. Notes 5.1) Red particles are receding, blue are approaching. |
|
|
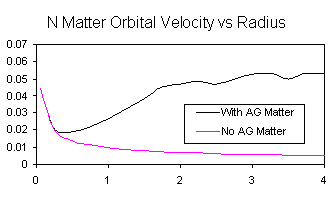
6) If the anti-gravity matter rotation is strong enough the velocity of a small normal matter particle in a circular orbit increases with radius. This is the anti-gravity matter vortex effect. A rotation of the anti-gravity matter decreases its density and increases gravity. With the right rate of rotation the normal matter orbital velocity can become fairly constant over a wide range of radii. Notes 6.1) The outer end of the orbital velocity profile is affected by the fact that in the simulation the anti-gravity matter particles tend to settle into shells. |
|
|
7) The simulation is then modified as follows:- 1. The anti-gravity matter particles are removed. 2. An extra gravitational force is added to approximately reproduce the gravitational effect of a fixed anti-gravity matter hole and an anti-gravity matter vortex as shown above. 3. Many smaller normal matter particles are added. 4. An artificial AGM Drag is introduced which slows the normal matter particles except when they are following close behind other normal matter particles. This has the effect of drag and wake. 5. A start up routine is carried out and a ball-and-disk galaxy shape is produced. 6. Further results from the simulation are shown in Galaxy simulation – 3 clusters |
|
|
** = As pointed out by my brother Geoff. |
|
|
Copyright © Tim E Simmons 2006, 2009 |
|