|
|
Basic Maths |
|
|||||
††††††††††††††††††††††††††††††††††††††††††††††††††
|
Definitions and
Assumptions Gravitational constant for normal matter to normal matter attraction = Gnn = conventional G Gravitational constant for normal matter to anti-gravity matter repulsion = Gna Gravitational constant for anti-gravity matter to anti-gravity matter repulsion = Gaa The background density of anti-gravity matter = Dab Assume that anti-gravity matter is cold and AGM Pressure is negligible. |
|||||||||||||||||
|
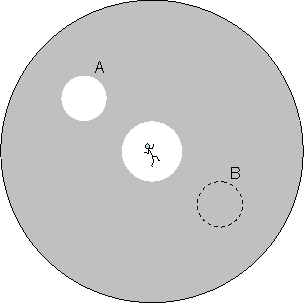
Consider a universe containing anti-gravity matter and an observer.† Assume that all the matter in the universe is at low energy and at equilibrium.† The anti-gravity matter is spread out evenly around the universe.† Any local disturbance to the anti-gravity matter caused by the observer is symmetrical around the observer.† Between that local disturbance and infinity the anti-gravity matter is at constant density in all directions.† The repulsion that the observer feels from the anti-gravity matter all around balances out and the net result is the observer feels nothing. Now imagine we remove the anti-gravity matter in the region of space marked A.† The observer feels nothing from A because it is empty but does feel an unbalanced repulsion from the volume of anti-gravity matter opposite A that is marked B. The effect is that the observer feels a net attraction to A.† The effect is exactly the same as if the universe was empty except for the observer and an equivalent mass of attractive matter filling volume A.† This equivalence is used in later calculations. |
|||||||||||||||||
|
2) What if the
observer is inside the region with no anti-gravity matter?
effective equivalent mass is
proportional to However the effect of that equivalent mass on the observer is governed by the inverse square law, so net force on the observer due
to gravity is proportional to† That is, the observer feels a gravitational attraction to the centre which is proportional to the distance from the centre.† The observer could counteract that force and remain at radius r if he was in a circular orbit.† If he was in a circular orbit at velocity v centripetal acceleration = acceleration due to gravity, which is proportional to the force due to gravity and and v is proportional to r That is, the circular orbital velocity is proportional to r.† This means that normal matter objects in a circular orbit within the sphere take the same amount of time to complete an orbit independent of radius.† The important consequence of this is that objects at different radii will orbit in formation and remain in formation. |
|||||||||||||||||
|
Incorrect.† We know the observer will feel something because the balance described in 1) above has been broken.† So whatís wrong with the shells argument? Actually nothing is wrong with it.† Itís just that usually the shells argument is applied when the observer is inside a finite body like a planet.† The shells can stack all the way up to the surface of the body and then the analysis stops.† However in this situation the shells stack all the way out to infinity.† The problem is that the shell at infinity is just a significant to the analysis as any other shells.† This is because the effect of any given particle in the shell goes down with the square of distance, but the total mass of the shell goes up with the square of distance.† The result is that we canít just ignore infinity because itís a long way away.† We have to deal with it properly. |
|||||||||||||||||
|
|
|||||||||||||||||
|
Hereís how to evaluate the effect of that
unbalanced volume of anti-gravity matter.†
Consider a ring around the axis that subtends angle
= force on observer of mass m at
centre from that ring = total force on observer of mass
m at centre = (note that the result is now independent of R) total force on observer of mass
m at centre = = The first term integrates to zero because the curve is symmetrical about the x-axis.† Therefore:- = The integral evaluates to total force on observer of mass
m = = = Note that this force is equal in strength but opposite in direction to the force that would be generated by a sphere of anti-gravity matter radius r located at the centre.† This supports the equivalence principle described in 1) above.† The force is also proportional to r as described in 2) above. |
|||||||||||||||||
|
4) The
attraction/repulsion grid This leads to the attraction/repulsion grid shown on the right. |
|
||||||||||||||||
|
5) Why is there a step
change in the density of anti-gravity matter at the AGM Boundary around a
normal matter object?
(force due to attraction to the volume of reduced density anti-gravity matter) = (force due to repulsion from the normal matter object) The reduction in density of anti-gravity matter at radius greater than r will have no effect on the anti-gravity matter particle at r because of the shells argument referenced above. (total reduction in
anti-gravity matter mass inside a sphere of radius r) x (total reduction in
anti-gravity matter mass inside a sphere of radius r) =† This is independent of r. If this is true for one particle at radius r where density is reduced, then at any radius greater than r there cannot be any reduction in anti-gravity matter density.† Hence there must be a step change in density.† (This explanation originally provided by brother Geoff) |
|||||||||||||||||
|
6)
Where is a normal matter objectís AGM Boundary?
Force on an observer of mass m
within a sphere from which the anti-gravity matter has been removed = By a similar argument if we replace the observer with an anti-gravity matter particle of mass m Force on an anti-gravity matter
particle of mass m within a sphere from which the anti-gravity matter has
been removed = Now take the situation on the right.† A large normal matter object of mass M has been placed in the universe and is repelling the anti-gravity matter and generating an AGM Boundary of radius r.† Consider a particle of anti-gravity matter of mass m which is in equilibrium at the boundary.† The attraction the particle feels towards the hole equals the repulsion the particle feels from the normal matter object.† Therefore:-
That is, the mass of anti-gravity matter missing from the hole
equals the mass of the central normal matter object times The radius of the AGM Boundary
= |
|||||||||||||||||
|
7) What defines the
AGM Exclusion Density? The AGM Exclusion Density is the density of normal matter that will completely exclude anti-gravity matter.† An example of this is given by the mass of the normal matter object in section 6 above divided by the volume within its AGM Boundary.† Note that in the diagram in section 6 the normal matter object is concentrated at the centre, but it would have the same gravitational effect if it was spread out over the volume within the AGM Boundary (because it could be imagined as being composed of a set of concentric shells which would each have the gravitational effect of being concentrated at the centre).† Therefore in these calculations we might be modelling a concentrated object like a star or a diffuse object like a molecular cloud. Therefore from section 6 above:- AGM Exclusion Density =† |
|||||||||||||||||
|
8) What effect
would the anti-gravity matter have on a small normal matter object at a large
objectís AGM Boundary? A normal matter object of mass m at the AGM Boundary (radius r) of for example a star with mass M feels an attraction to the star and an attraction to the anti-gravity matter hole. Total attraction = But and therefore†
Therefore total attraction = = = For example if the three G constants were equal the normal matter objectís attraction to the star would be doubled at the AGM Boundary. |
|||||||||||||||||
|
The Maths above deals with the case where AGM Pressure is
not significant and Pab can be assumed to be zero.† In Investigation
it is explained that this assumption is more likely to apply at large
scale.† At small scale it can be
assumed that AGM pressure is dominant and Gaa is
zero.† The maths that deals with that
situation is set out in Investigation
> Maths with AGM Pressure. |
|||||||||||||||||
© Copyright Tim E Simmons 2008 to
2015. Last updated 27th July 2015.†
Major changes are logged in AGM Change Log.
 1)
What gravitational effect does anti-gravity matter have?
1)
What gravitational effect does anti-gravity matter have? Now
imagine that the observer is within a spherical volume that contains no
anti-gravity matter, and located a distance r from the centre of that
volume.
Now
imagine that the observer is within a spherical volume that contains no
anti-gravity matter, and located a distance r from the centre of that
volume.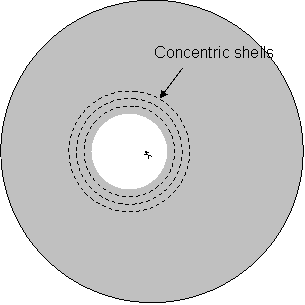 3)
Wait a minute! The shells argument can be applied to the situation in 2) above
to prove that all the anti-gravity matter outside the spherical volume and
all the way to infinity will have zero net effect.
3)
Wait a minute! The shells argument can be applied to the situation in 2) above
to prove that all the anti-gravity matter outside the spherical volume and
all the way to infinity will have zero net effect.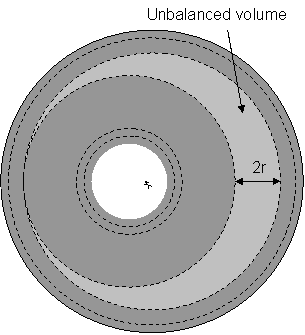 And hereís a way to deal with that
infinity.
And hereís a way to deal with that
infinity.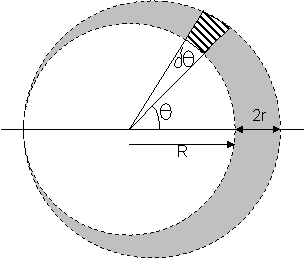 mass of anti-gravity matter in the ring
=
mass of anti-gravity matter in the ring
= 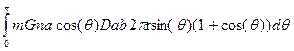
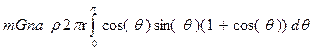
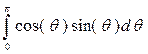
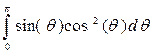
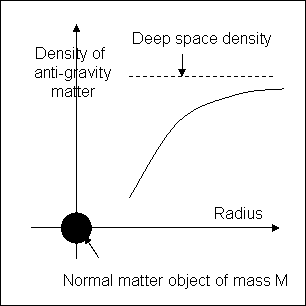 Imagine that there isnít a step change
and at equilibrium the density of anti-gravity matter varies smoothly as
shown on the right.
Imagine that there isnít a step change
and at equilibrium the density of anti-gravity matter varies smoothly as
shown on the right.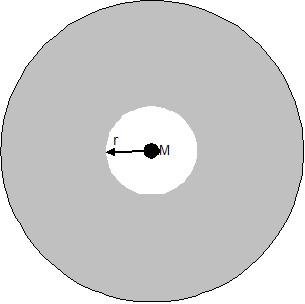 From section 3 above we have:-
From section 3 above we have:-