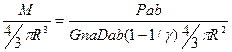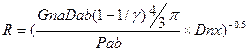|
|
Maths with AGM
Pressure |
|
|||||
|
This page describes an analysis of the behaviour of anti-gravity matter around a small central normal matter object when AGM Pressure is involved. This analysis is much simplified by the observation described in Investigation that for small scale phenomena anti-gravity between anti-gravity matter particles can be ignored. In the analysis we assume that Gaa = 0. Definitions and
Assumptions Gravitational constant for normal matter to normal matter attraction = Gnn = conventional G Gravitational constant for normal matter to anti-gravity matter repulsion = Gna Gravitational constant for anti-gravity matter to anti-gravity matter repulsion = Gaa = 0 The background density of anti-gravity matter = Dab The AGM Exclusion Density = Dnx The background pressure of anti-gravity matter = Pab Assume monatomic adiabatic expansion where |
|
Assume anti-gravity matter is arranged spherically symmetrically around a central normal matter object of mass M. Radius variable = r Anti-gravity matter density at any radius = Anti-gravity matter pressure at any radius = p For any thin concentric spherical shell weight (outwards) is supported by change of pressure. 1)
The equation for adiabatic expansion of anti-gravity matter as pressure decreases 2)
Therefore 3)
But from 1) and 2) 4)
Integrate 5)
When r = 6)
At the AGM Boundary let r = R, p = 0 and from 5) and 6) 7)
8)
R = and 9)
AGM Exclusion Density = Dnx
= and therefore 10) Therefore from 8) the radius of the AGM Boundary is proportional to M, and from 10) inversely proportional to the square root of AGM Exclusion Density. |
© Copyright Tim E Simmons 2010 to
2015. Last updated 27th July 2015.
Major changes are logged in AGM Change Log.
 What’s
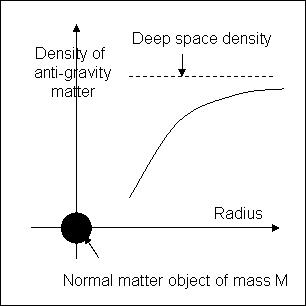
the relationship between anti-gravity matter pressure and radius?
What’s
the relationship between anti-gravity matter pressure and radius?