AGM Home	Behaviour	Evidence	Simulations	Investigation	Objections	Problems
				Introduction to an AGM Pressure Simulation

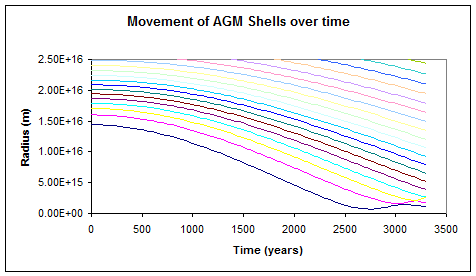
This page is part of a sequence of logical steps that are described in Investigation. A spreadsheet simulation has been produced to investigate the influence of AGM Pressure. This simulates the behaviour of antigravity matter around a central object under the effects of gravity, pressure and inertia. In the simulation the antigravity matter is divided into a series of concentric spherical shells. The shells expand or contract over time but always remain concentric with the central object. The simulation only allows one degree of freedom of movement for each shell. However it should be reasonably accurate representation of the behaviour of antigravity matter in three dimensional space in cases where antigravity matter remains spherically symmetrical. Some example results from this are shown below. 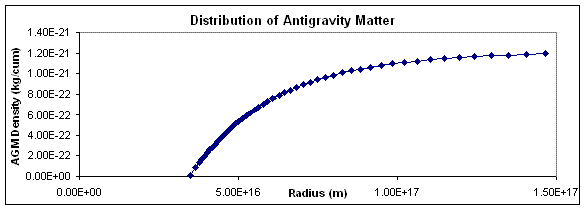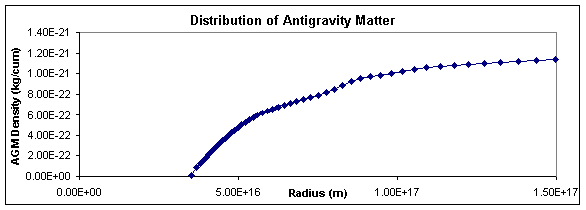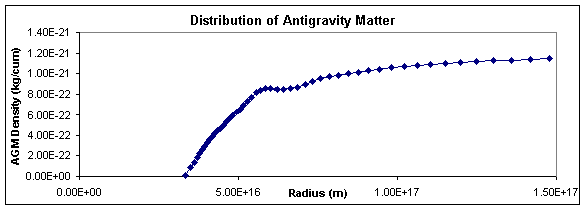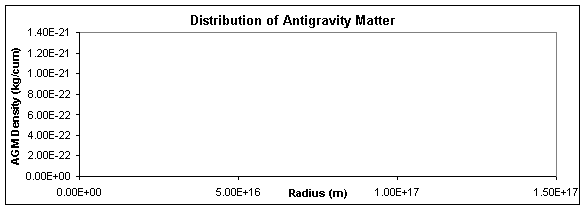Each of these shows the distribution of antigravity matter when at equilibrium around a central normal matter object. 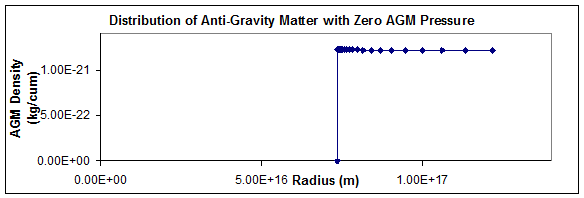The first shows antigravity matter that has zero pressure. 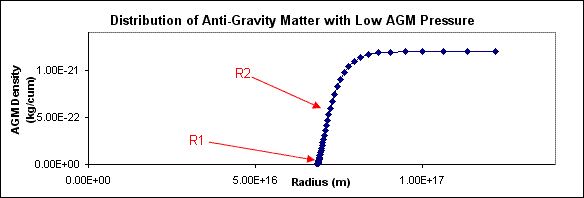The second shows the effects of low AGM Pressure. 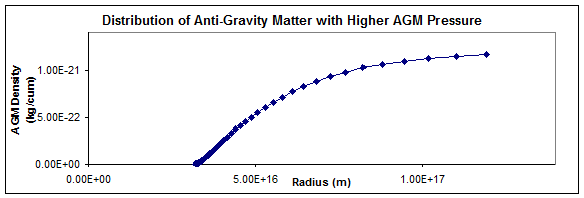The last shows the effects of higher AGM Pressure. An Adiabatic Index of 5/3 is used for all plots. Antigravity matter is assumed to behave like an ideal monatomic gas.
Central normal matter mass = 2 × 10^30 kg Gna = 6.67 × 10^-11 cu m/kg s^2 Gaa = 6.67 × 10^-11 cu m/kg s^2 Dab = 1.2 × 10^-21 kg/cu m Pab = 0
Central normal matter mass = 2 × 10^30 kg Gna = 6.67 × 10^-11 cu m/kg s^2 Gaa = 6.67 × 10^-11 cu m/kg s^2 Dab = 1.2 × 10^-21 kg/cu m Pab = 1.0 × 10^-20 N/sq m
Central normal matter mass = 2 × 10^30 kg Gna = 6.67 × 10^-11 cu m/kg s^2 Gaa = 6.67 × 10^-11 cu m/kg s^2 Dab = 1.2 × 10^-21 kg/cu m Pab == 1.0 × 10^-18 N/sq m
AGM Pressure pushes the AGM Boundary inwards. In Investigation we use two ways to define the AGM Boundary. These are labelled R1 and R2 above. R1 is point at which the density of antigravity matter reaches zero. R2 is the point at which density is half the background density. The AGM Exclusion Density of a normal matter object is given by the mass of the object divided by the volume within its AGM Boundary. Each of the three cases above gives a value for the AGM Exclusion Density under different conditions. It can be seen that the AGM Exclusion Density increases with AGM Pressure.
The AGM Pressure Simulation is also a dynamic simulation. That is, it simulates the dynamics of antigravity matter. An example of this is shown on the right. At T=0 the antigravity matter is in equilibrium with a distribution similar to the third case above. The deep space antigravity matter density is suddenly reduced by about 5%. Waves are generated that flow through the antigravity matter.
In this simulation at Time=0 the antigravity matter has a fairly low AGM Pressure and is in equilibrium around a central star which has 10 time the mass of the sun. The AGM Pressure is suddenly raised by a factor of 1000, simulating the effect of sudden heating of the antigravity matter. The result is that the antigravity matter shells are forced inwards and cause a high density splash in the centre. The splash starts to occur about 2700 years after the original heating event.

© Copyright Tim E Simmons 2008 to 2015. Last updated 28^th July 2015. Major changes are logged in AGM Change Log.